Keď mal rok 360 dní a hľadali sa odmocniny
Musíme sa presunúť v čase asi o 4 000 rokov nazad a v priestore do oblasti dnešného Iraku. V tom čase bola oblasť Mezopotámie kolískou civilizácie. Dnes bude reč o „Sillicon Valley“ doby bronzovej. O Babylone.
Išlo o mesto s vyspelou kultúrou a rozvinutou vedou. Astronomické pozorovania, zápis pomocou klinového písma na hlinené tabuľky, šesťdesiatková číselná sústava. Mnohé poznatky využívame dodnes.
Práve v Babylone sa rozhodli kruh rozdeliť na 360 častí. Ako sa to stalo? Precíznym pozorovaním a zapisovaním pozície Slnka pri východe a západe. Podarilo sa im stanoviť letný a zimný slnovrat, rovnodennosť. Zistili, že celý cyklus sa opakuje po 360 dňoch. Cyklický dej zapísali do kruhu a rozdelili ho na 360 dielov – dní. Odtiaľ pramení aj v súčasnosti zaužívané delenie kruhu na 360 dielov – stupňov. 360 je navyše veľmi príjemné číslo (obzvlášť v šesťdesiatkovej sústave). Dobre sa delí. Má spolu 24 deliteľov, medzi nimi napr. 12.
360/12 = 30, čiže 12 mesiacov, 30 dní v mesiaci
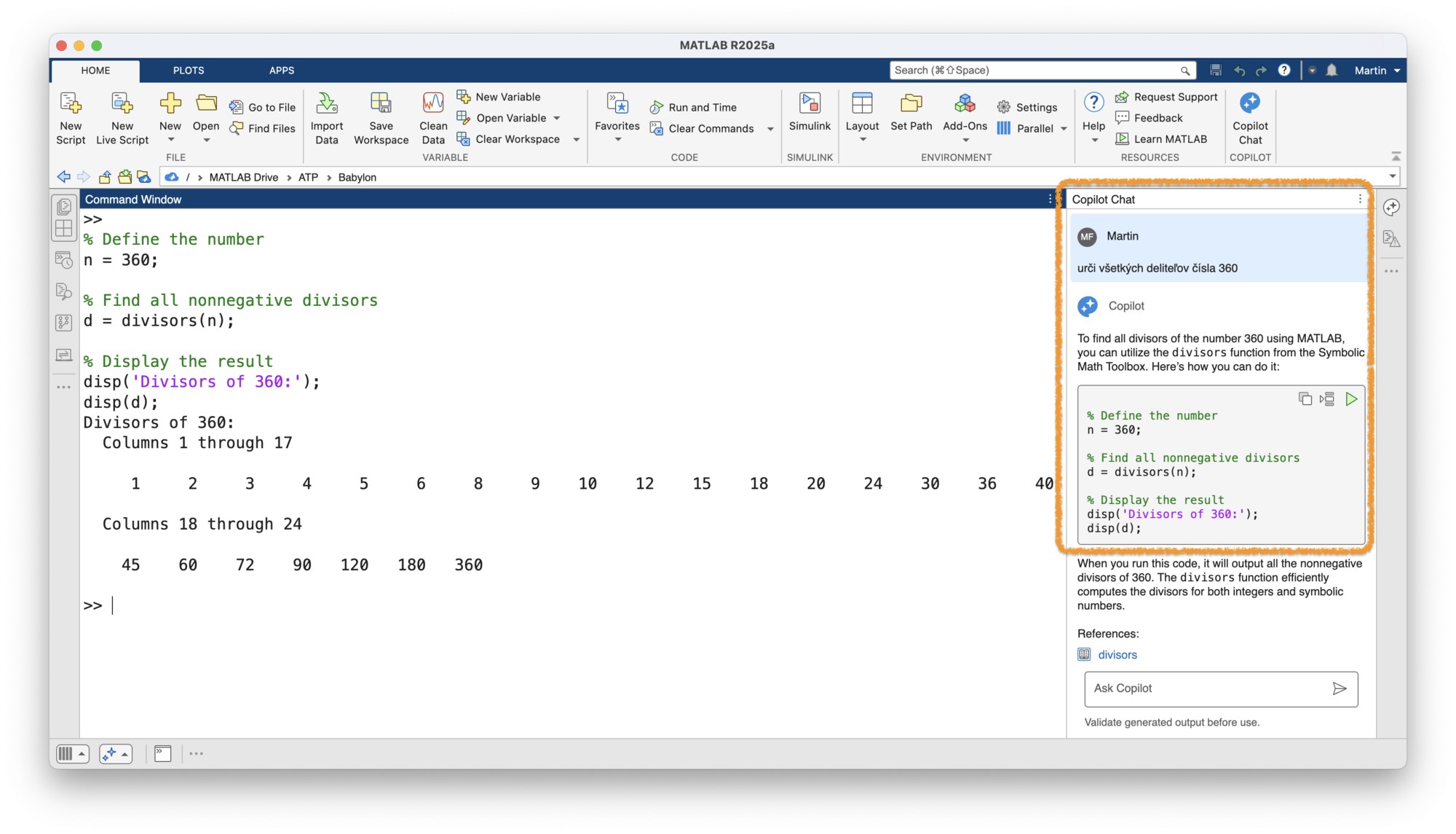
Ako zistiť všetkých deliteľov? Zavolám si na pomoc MATLAB Copilot. Viac o novinke píše kolega Michal Blaho v tomto čísle časopisu.
Obr. 1 MATLAB Copilot – výpočet deliteľov čísla 360 (v galérii)
Ako o znalostiach Babylončanov vieme? Sú zapísané na hlinených tabuľkách klinovým písmom. Prežili tisícročia. Dnes ich vieme dešifrovať (pomáha už aj UI) a tak objavovať, na čo všetko ľudia v dávnej minulosti prišli a s čím bežne pracovali. Na pôde univerzity Yale sa nachádza malý, no mimoriadne vzácny artefakt – hlinená tabuľka s označením YBC 7289 [1].
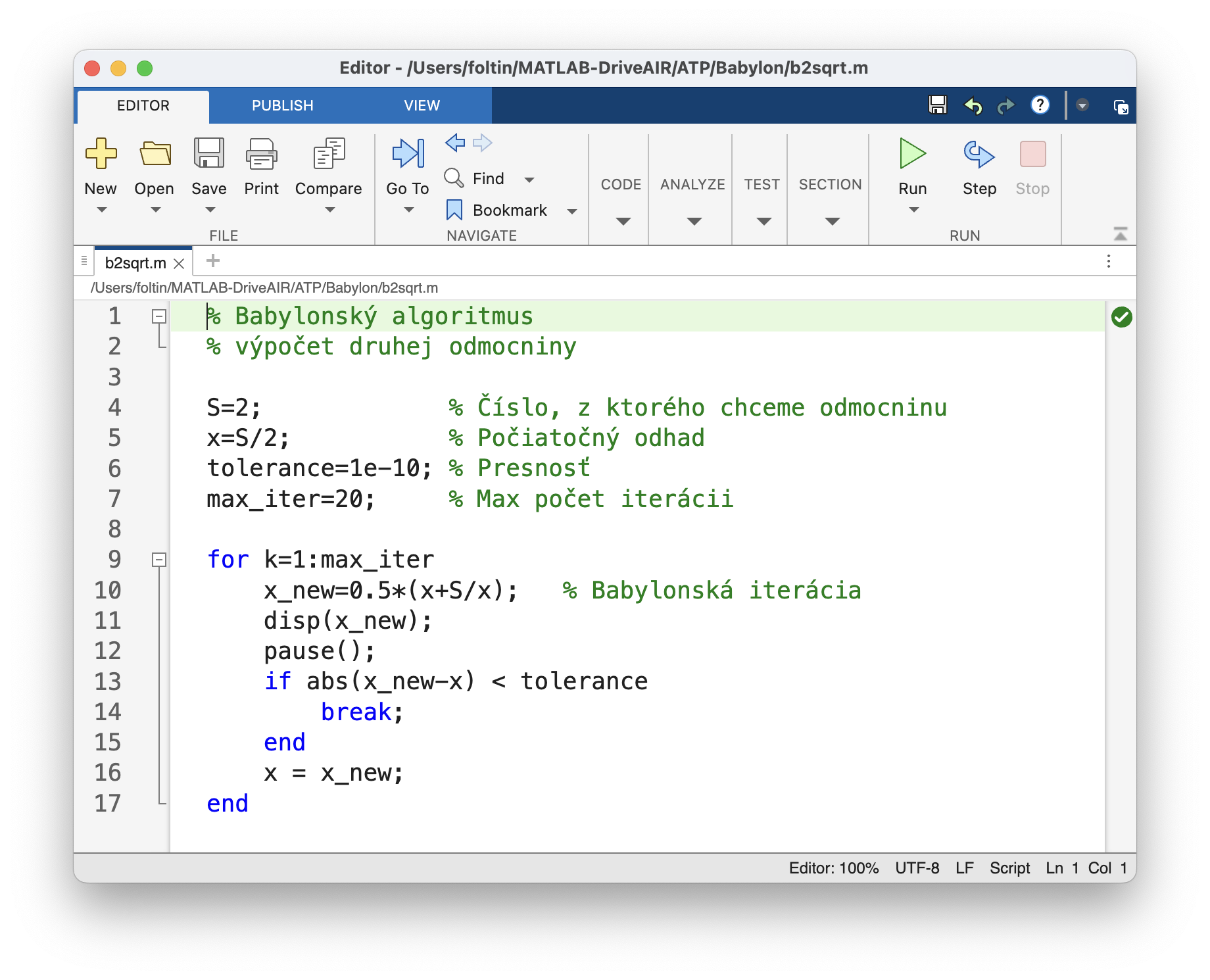
Ak by ste ovládali klinové písmo, vedeli by ste z nej prečítať algoritmus na výpočet druhej odmocniny. Nie je to program, ako ho poznáme dnes, ale v číselnom zápise sa dajú jasne rozoznať jednotlivé kroky výpočtu druhej odmocniny z čísla 2. A výsledok? 1,41421296. Porovnajte si ho so svojou kalkulačkou – odchýlka je zanedbateľná. To všetko len pomocou rydla, hliny a najmä dôvtipu pred viac ako 3 500 rokmi. Babylonský algoritmus sa v dnešnom matematickom jazyku dá zapísať takto:
![]()
kde S je číslo, ktoré odmocňujeme, n – iteračný krok, x – odhad druhej odmocniny.
V uvedenej alebo mierne modifikovanej forme sa využíva v numerickej matematike dodnes. Pravdepodobne na jeho základe počíta odmocninu aj vaša kalkulačka.
Obr. 2 Babylonský algoritmus na výpočet druhej odmocniny v jazyku .m (v galérii)
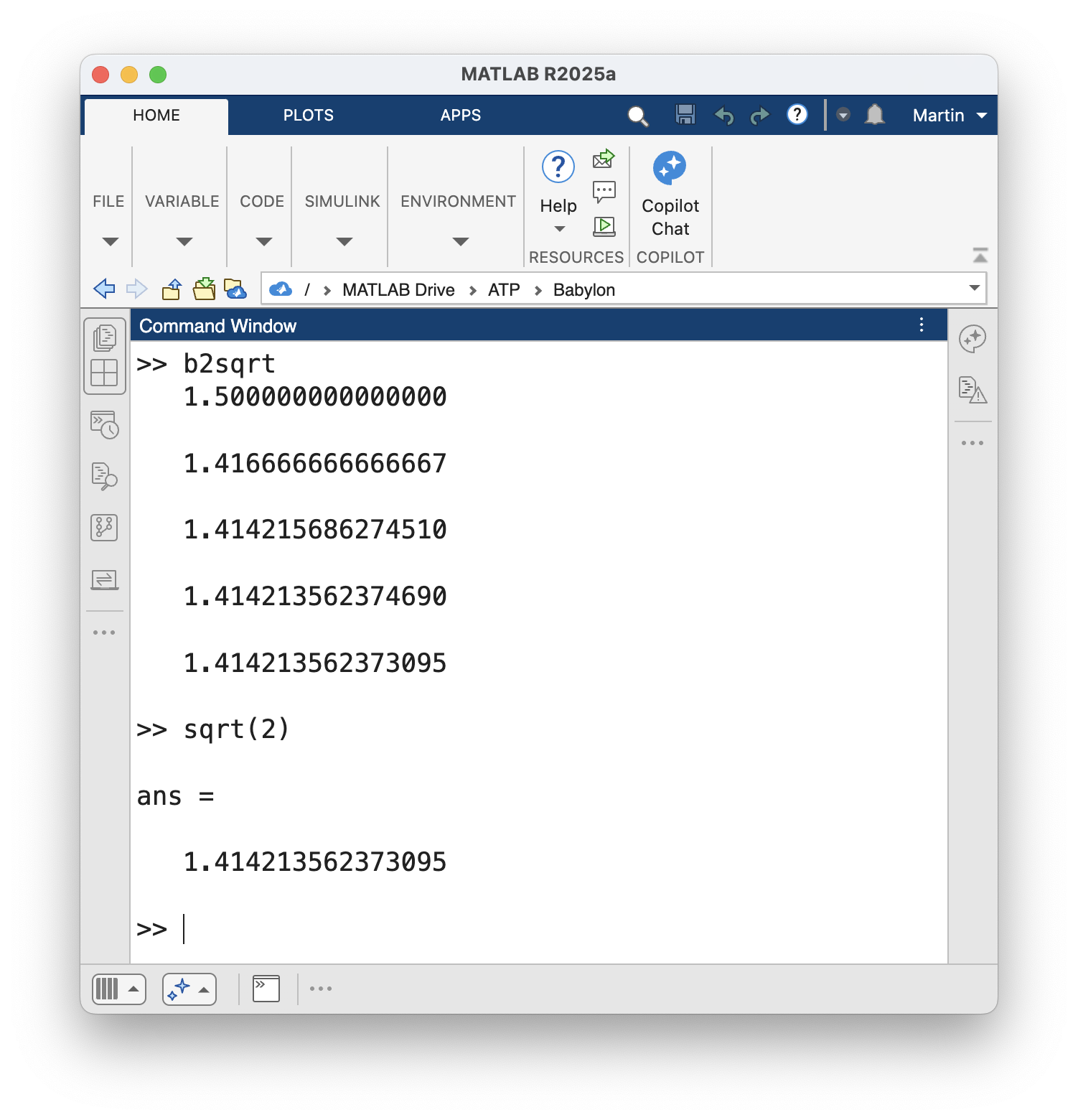
Po pár krokoch sa dopracujeme k takejto hodnote.
Obr. 3 Iteračné kroky pri výpočte √2. Na porovnanie výstup z funkcie sqrt(2) (v galérii)
Babylončania netušili, že odmocnina z 2 je iracionálne číslo. Na to prídu až o 1 000 rokov neskôr Pytagorejci, čím destabilizujú filozofiu celej svojej školy.
Prečo vlastne píšem o algoritme na výpočet odmocniny? Pripravujem si tak pôdu na príbeh, ktorý sa odohral začiatkom 17. storočia. Je to príbeh o logaritme a logaritmických tabuľkách. Bez uvedeného algoritmu by sa Napierovi a Briggsovi veľmi ťažko počítali prvé logaritmické tabuľky. Tento fascinujúci príbeh si priblížime v ďalšej časti.
Poznámka pod čiarou
Domnievam sa, že výučbu matematiky treba obohatiť o príbehy z histórie. Obvykle nám dajú odpoveď na základnú otázku: A načo mi to bude? Ľudia v histórii riešili reálne problémy, kde im matematika pomáhala. Babylončania boli zdatní geodeti a výpočet dĺžky uhlopriečky štvoruholníka bola častá úloha. Takže odmocnina. Astronomické výpočty s využitím pravouhlých trojuholníkov. Výpočet dĺžky prepony – odmocnina. Treba si uvedomiť, aké technické vybavenie mali v danej dobe. Nezaškodí replikovať postupy. Som presvedčený o tom, že pomocou zážitkov a príbehov sa dá budovať pozitívny vzťah k matematike.
#MatikaBezStresu
Literatúra
[1] Wikipedia. [online]. Citované 8. 8. 2025.
[2] Mackenzie, D.: Príbeh matematiky v 24 rovniciach. Bratislava: Ikar 2021.
Martin Foltin
https://www.linkedin.com/in/mfoltin/