Keď sa z násobenia stalo sčítavanie
Koniec 16. a začiatok 17. storočia, neskorá renesancia. Vedecká revolúcia sa začína rozbiehať. Éra veľkých námorných objavov, navigácia, astronómia, staviteľstvo, dane. Každá z činností vyžadovala jeden v tej dobe náročný úkon – násobenie. Nehovoríme o malej násobilke, ale o násobení veľkých čísel s niekoľkými desatinami. Skúste ručne vynásobiť niekoľko viacciferných čísel. Vyžaduje to dookola násobiť malé čísla a následne sčítavať. Desiatky a možno stovky operácií. S množstvom rastie pravdepodobnosť chyby.
O úzkom mieste sa vedelo. Predpokladám, že s riešením si lámalo hlavy viacero múdrych hláv. John Napier, škótsky šľachtic, však udrel kladivom po hlavičke. Ako aristokrat si mohol dovoliť užívať rozsiahle majetky, ale svoj život zasvätil matematike a mechanike. Jeho objav spočíva v tomto pravidle: Ľubovoľné číslo môžeme zapísať ako mocninu zvoleného základu. Znie to zložito. Takto to vyzerá v matematickom zápise:
![]()
Ak by sme chceli byť konkrétny, tak si uveďme príklad so základom 10 (k = 10). Číslo 1 000 môžeme zapísať ako 103.
OK, máme začiatok. Napier si však uvedomil, že platí:
![]()
A zrazu máme z násobenia sčítavanie. Skúsme si to na jednoduchom príklade.
![]()
Princíp pomerne jednoduchý. Má však háčik. Ako zistiť mocninu ľubovoľného čísla pri základe 10? Pri číslach ako 100 alebo 1 000 je to úloha triviálna. Čo však s takým číslom ako 20? Napier si uvedomil, že ak má byť jeho objav užitočný, bude musieť vymyslieť mechanizmus, ako transformovať čísla – logaritmovať. To bol podnet na vznik prvých logaritmických tabuliek. Napier ručne počítal logaritmy od 1 až po 107. Trvalo mu to roky. Neboli to však tabuľky pri základe 10. Bolo to trošku komplikovanejšie. Skutočne použiteľné logaritmické tabuľky so základom 10 vytvoril až Henry Briggs, Napierov kamarát. Spoločne sa zhodli na tom, že základ 10 bude pre praktické využitie najlepší. Nasledovali ďalšie roky práce, kým tabuľky uzreli svetlo sveta. Ako však postupoval pri ich tvorbe? Briggs si stanovil dva body (zvolil dve čísla), ktoré ide ľahko logaritmovať. Ako príklad môžeme použiť 1 a 10.
![]()
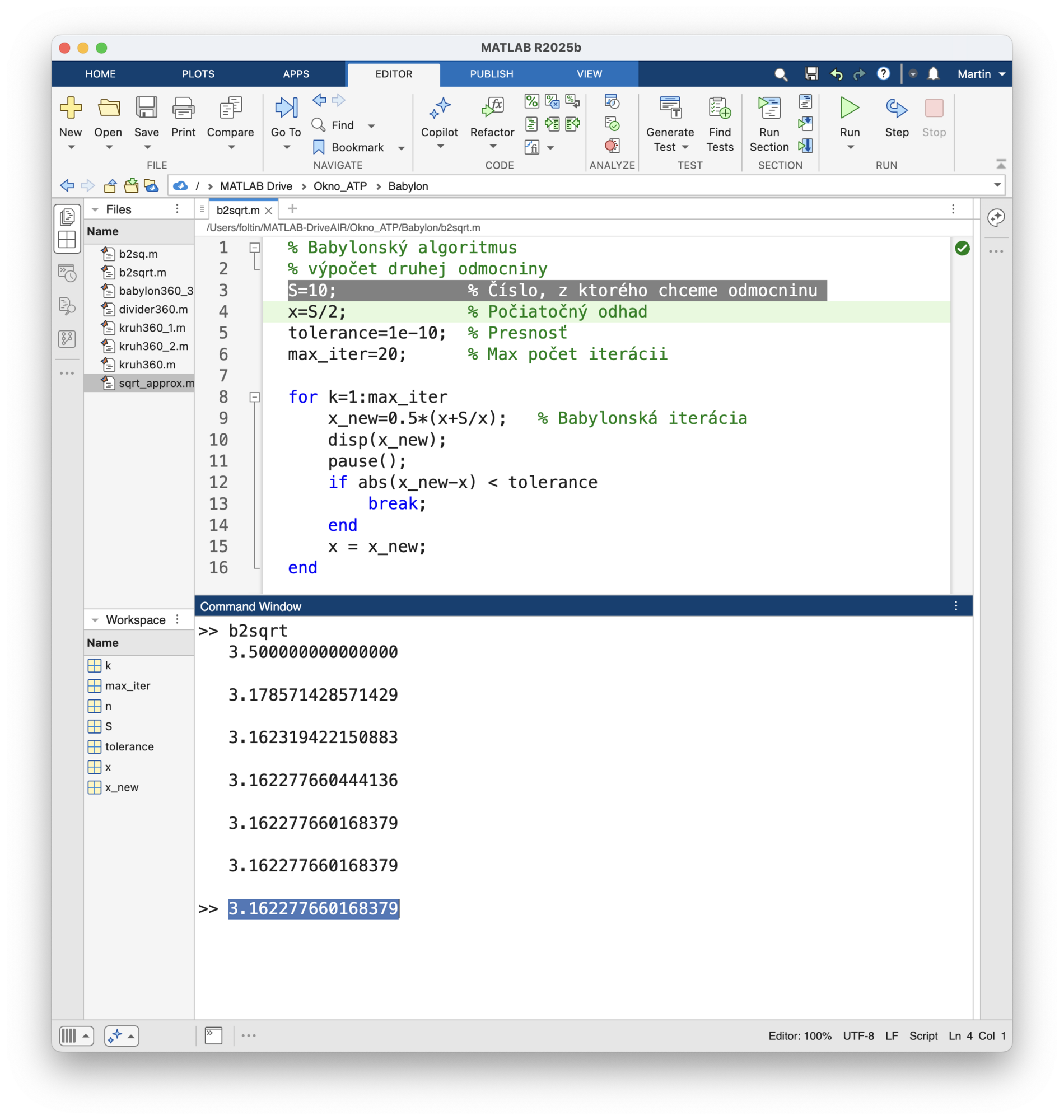
Mocniny sú teda 0 a 1. Určil stred – 1/2. Koľko je 10(1/2)? No to je predsa druhá odmocnina z 10. Fajn a čo s takým číslom? Ako spočítať druhú odmocninu z 10? Siahneme po Babylonskom algoritme, o ktorom som písal v predošlej časti.
Tak a máme ďalší zápis do logaritmickej tabuľky. Vieme, že 3,162277660168379 sa zlogaritmuje na 0,5. Rozdelíme interval 0 a 1/2 na polovicu a dostaneme sa na 1/4. 10(1/4) je štvrtá odmocnina z 10, ale aj druhá odmocnina z druhej odmocniny z 10. Dostaneme číslo 1,778279410038923. A máme ďalší riadok v logaritmických tabuľkách. Takýmto postupom Briggs vytvoril ucelené dielo – Arithmetica Logarithmica. Dnes voľne dostupné ako scan. Naživo sa dá vidieť napr. v Cambridge University Library alebo British Library v Londýne.
A ako to fungovalo v praxi? Astronóm potreboval vynásobiť dve čísla. Napr. 372 x 57. Našiel obrazy čísel v tabuľkách: log(372) = 2,570542 log(57) = 1,755875 Sčítal ich: 2,570542 + 1,755875 = 4,326417 A následne toto číslo odlogaritmoval. Získal tak číslo ~21 204. Násobenie a delenie sa tak výrazne zjednodušilo a zrýchlilo. Logaritmy sa stali základným nástrojom inžiniera na 350 rokov. K zvýšeniu rýchlosti počítania dopomohlo logaritmické pravítko (rok 1622), ktoré patrilo k výbave astronautov NASA, a to aj v rámci programu Apollo.
Súmrak nad tabuľkami a pravítkami priniesli až polovodiče a príchod kalkulačiek. Prvý zlom nastal s uvedením HP-35 (1972). Vedela logaritmovať. Bola však príliš drahá (okolo 400 USD). O dva roky neskôr prichádza TI-SR40 za 170 USD a v roku 1976 sa definitívne končí éra, ktorú začal Napier a Briggs. Na trh prichádza TI-30 za 25 USD, ktorej sa predalo viac ako 10 miliónov kusov. #MatikaBezStresu
Martin Foltin
https://www.linkedin.com/in/mfoltin/